01-16 최소 제곱법과 추세선
선형 회귀
def) 선형 회귀 (Linear Regression): 주어진 데이터를 가장 잘 설명하는 합리적인 선형함수를 찾는 문제
어떤 한 상인의 노동 시간에 따른 매출액 데이터가 있다고 해보겠습니다.
| 하루 노동 시간 | 매출 |
|---|---|
| 1 | 25000 |
| 2 | 55000 |
| 3 | 75000 |
| 4 | 110000 |
| 5 | 128000 |
| 6 | 155000 |
| 8 | 210000 |
이 표에서 7시간을 일했을 때의 매출액과 9시간 이상 일을 했을 때의 매출액은 나타나있지 않습니다. 그렇다면 주어진 데이터를 바탕으로 7시간, 9시간 일했을 때의 매출액을 예측하려면 어떻게 해야 할까요? 가장 간단한 방법은 주어진 데이터들 간의 상관관계를 선형함수의 형태로 나타내는 겁니다. 이를 선형 회귀라고 합니다.
대개 선형 회귀는 학습 데이터가 3개 이상일 때 의미가 있다고 판단합니다. 선형함수를 가정했으므로 우리의 모델을 $f\left(x\right) = Wx + b$로 놓고, 이를 가장 잘 표현하는 계수 $W$와 $b$를 찾는 것이 선형회귀의 큰 틀입니다.
학습
ML에서 학습이라 함은 주어진 데이터를 이용해 모델이 다루는 함수를 수정하는 것을 뜻합니다. 이를 선형회귀에 적용해보면 학습을 통해 가장 합리적인 두 계수 $W$와 $b$를 도출하는 과정이 되겠습니다.

그렇다면 ML 모델을 학습하는 과정에서 현재 우리의 모델이 실제 값에서 얼마나 잘못되었는지를 나타내는 방법이 필요합니다. 지난 포스트에서, 이를 나타낼 때 오차(error)의 개념을 쓰되, 비용(cost) 또는 손실(loss)이라고 나타낸다고 했습니다. 이를 달리 설명하면, 우리의 모델이 정확하지 않다면 높은 비용이 발생합니다. 따라서 비용을 최소화하는 방향으로 학습이 이루어지게 됩니다.
최소제곱법
def) 최소제곱법 (Least Square Method): 모든 데이터에 대한 $\left(real-prediction\right)^2$의 합으로 비용을 계산해 이를 최소화하는 방법 a.k.a. 최소자승법
ML 분야에서 오차를 나타낼 때 가장 자주 쓰이는 것이 평균 제곱 오차(MSE)라고 했습니다. 이를 이용해 다음 식을 최소화하는 $W$와 $b$를 찾는 방법을 최소제곱법이라 합니다. 데이터가 총 $m$개 주어졌다고 하면 비용은 아래와 같이 계산될 것입니다.
$$cost\left(W,b\right)=\frac{1}{m}\sum_{i=1}^{m}\left(H\left(x_i\right)-y_i\right)^2$$
$$\left(where H\left(x\right)=Wx+b\right)$$
비용 예제
$W=1$, $b=2$일 때의 비용을 계산해보겠습니다. ($y=x+2$)
| X | Y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
$$cost\left(W,b\right)=\frac{1}{m}\sum_{i=1}^{m}\left(H\left(x_i\right)-y_i\right)^2$$
$$=\frac{\left(3-2\right)^2+\left(4-4\right)^2+\left(5-6\right)^2}{3}=frac{2}{3}$$
그렇다면 비용을 더 줄이기 위해 어떻게 학습을 시켜야 할까요?
경사하강법
def) 경사하강법 (Gradient Descent): 기울기를 이용하여 비용을 줄이는 방법
미분을 이용하면 특정 값에서의 함수의 기울기를 구할 수 있습니다. 우리는 이 기울기를 최소화시키는 방법으로 비용을 줄일 수 있습니다. 예를 들어, 아래 그림을 보시면...
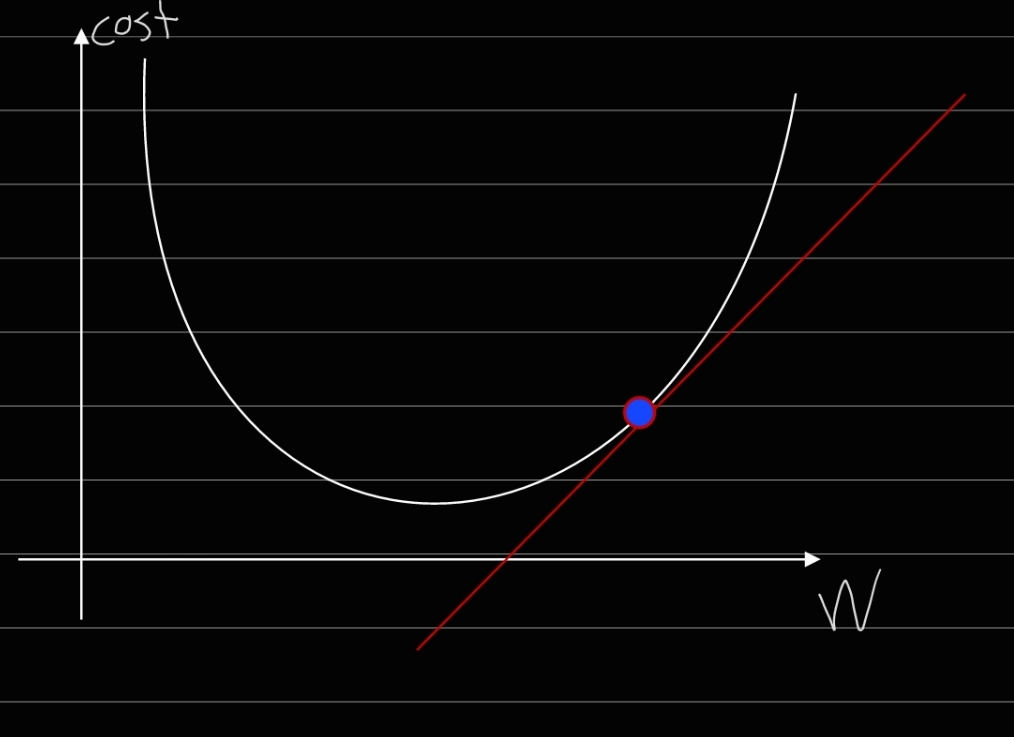
2차함수의 형태로 비용함수가 주어져 있습니다. 이 경우, 현재 점이 찍힌 곳의 기울기가 양수이므로, 가중치를 음수 방향으로 이동시키면 기울기를 최소화할 수 있습니다. 반대로 기울기가 음수일 경우, 가중치를 양수 방향으로 이동시켜 기울기를 최소화합니다.
그러면 간단하게 $H\left(x\right)=Wx$로 가장 간단한 형태로 가정해보겠습니다. 그러면 비용함수 MSE는 아래와 같이 계산됩니다.
$$cost\left(W\right)=\frac{1}{m}\sum_{i=1}^{m}\left(Wx_i-y_i\right)^2$$
그렇다면 $\left(Wx_i-y_i\right)^2$의 합을 최소화하는 방법을 찾아야겠죠? 아까 설명드렸듯이, 이 MSE 비용함수는 아래로 볼록하므로, 경사를 타고 내려가면 비용이 감소합니다. 따라서 비용함수를 $W$로 미분해 기울기를 구한 후, 기울기의 반대 방향으로 $W$를 업데이트합니다. 그런데 어느 정도의 크기로 이동하는 게 적절할까요? 너무 크게 이동하면 기울기 곡선의 반대 방향으로 더 높이 치솟을 수도 있겠죠? 반대로 너무 작게 이동하면 방향은 맞지만, 최소한의 비용에 도달하는 데 천년만년이 걸릴 수도 있습니다.
그래서 적절한 크기로 이동할 수 있게 학습률(learning rate, $\eta$)를 곱하여 이동합니다. 예를 들어, $\eta=0.01, W=7$일 경우,
W = W - 7*0.01와 같이 업데이트 할 수 있고, 이 과정을 반복하면, 가중치는 올바른 지점으로 수렴할 수 있습니다. 학습률은 ML 분야에서 가장 빈번하게 등장하는 기초적인 개념이니 잘 기억해두는 것이 좋습니다.
16일차 후기
비용과 손실 관련한 내용은 머신러닝을 공부하고 적용하는 내내 사용되는 개념이니 여기서 잘 잡고 넘어가야겠습니다. 학부 때 머신러닝 수업을 들을 때도 여기서 막히는 학생들이 꽤 많았던 걸로 기억하는데, 제가 써놓은 걸 다시 읽어보니 나도 제대로 이해하지는 않았구나 하고 반성하게 됩니다... 학생 여러분 공부 열심히 합시다...!
패스트캠퍼스 [직장인 실무교육]
프로그래밍, 영상편집, UX/UI, 마케팅, 데이터 분석, 엑셀강의, The RED, 국비지원, 기업교육, 서비스 제공.
fastcampus.co.kr
* 본 포스팅은 패스트캠퍼스 환급 챌린지 참여를 위해 작성되었습니다.
'[패스트캠퍼스 환급챌린지]딥러닝 > Chapter 1. 통계' 카테고리의 다른 글
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-17 데이터 추출 (0) | 2023.03.08 |
|---|---|
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-15 편향과 오차 (0) | 2023.03.06 |
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-14 최대 가능도 추정 (0) | 2023.03.05 |
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-13 확률분포의 추정 (0) | 2023.03.04 |
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-12 공분산과 상관계수 (0) | 2023.03.03 |