AI개발세발

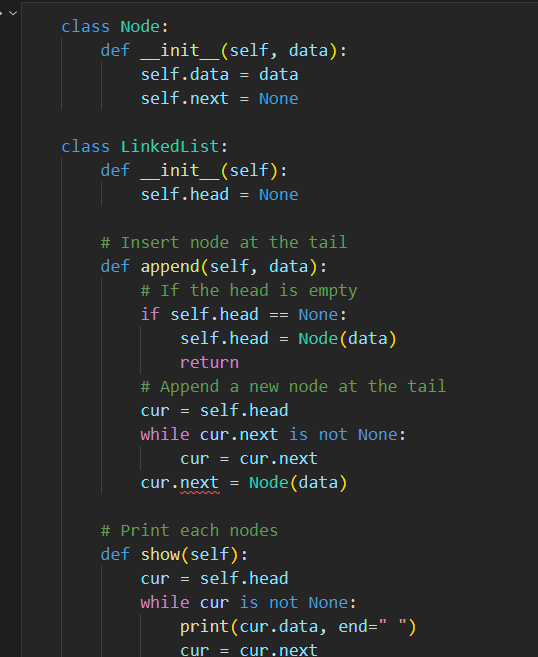
02-03 연결 리스트 def) 연결 리스트 (Linked List): 각 노드가 한 줄로 연결되어 있는 자료구조 지난 시간에 배열을 설명하면서 곁다리로 언급했던 연결 리스트에 대해 좀 더 자세히 알아보겠습니다. 각 노드는 (데이터, 포인터)의 한 쌍으로 묶여 있으며, 이러한 각 노드가 한 줄로 연결되어 있는 것이 연결 리스트입니다. 여기서 포인터는 다음 노드의 메모리 주소를 가리키는 역할을 합니다. 각 노드의 포인터가 다음 혹은 이전 노드를 가리키는 것을 연결성이라고 합니다. 연결 리스트를 이용하면 앞으로 배울 스택, 큐 등 다양한 자료구조를 구현할 수 있습니다. 다만, 우리가 데이터 사이언스와 ML 분야에서 주로 사용하는 파이썬은 연결 리스트를 활용하는 자료구조인 리스트(list)를 자체적으로 제공합..

02-02 배열 가장 기본적인 선형 자료구조로 배열(array)를 먼저 살펴보겠습니다. 배열은 일종의 표와 같이 여러 개의 변수를 담는 공간이자, 0부터 시작되는 인덱스(index)가 존재합니다. (인덱스는 순서 개념으로 보시면 되겠습니다. 파이썬을 다뤄보신 분들은 인덱스가 0부터 시작되는 것에 익숙하실 겁니다.) 아래 표에서 각각의 값마다 인덱스가 할당된 것을 볼 수 있습니다. 배열 자료는 자신이 원하는 특정한 인덱스에 직접적으로 접근할 수 있으며, 수행 시간을 시간 복잡도로 표현하면 $O\left(1\right)$입니다. 인덱스 0 1 2 3 4 5 6 7 8 값 25 75 83 59 24 72 55 17 42 배열의 특징 컴퓨터 부품 중 램(RAM)은 메인 메모리로써 저장장치 중에서는 읽고 쓰는 속..

Chapter 2. 딥러닝을 위한 자료구조 통계와 관련된 이론은 지난 포스트에서 끝났고, 오늘부터는 컴퓨터공학과 관련된 내용이 주를 이룹니다. 개인적으로 머신러닝을 깊게 파고들기 시작하면서 가장 아쉬웠던 부분이, 학부 당시 수업에서 머신러닝 기법과 그 적용 위주로만 수업을 들은 탓에 정작 그 기법으로 다뤄야 하는 데이터가 어떤 특성을 가지고, 그래서 어떻게 다루는 것이 더 효율적이고 올바른지를 전혀 알려주지 않았다는 겁니다(데이터 전처리(preprocessing)가 아니라 오늘부터 다룰 자료구조, 그 외에는 데이터베이스 등의 정보를 말하는 겁니다). 그래서 더더욱 이 챕터가 저에게 중요하게 다가오는 것 같네요. 저한테 왜 그랬어요 02-01 Data Structure 개요 자료구조 def) 자료구조 (D..

01-17 데이터 추출 자, 어느덧 통계 이론 파트의 마지막입니다. 그럼에도 이번 데이터 추출 부분은 그 중요성을 절대로 간과할 수 없는 부분입니다. ML 분야에서는 데이터를 랜덤으로 추출해야 하는 경우가 많기 때문입니다. 데이터 추출 예시 Case 1. 한 개의 원소 랜덤 추출 100개의 데이터 중 랜덤으로 1개를 추출하는 상황을 가정해보겠습니다(이를 데이터를 샘플링한다라고도 표현합니다). import numpy as np import random arr = np.arange(1, 101) sampled = random.choice(arr) print(sampled) 28 넘파이의 arange 함수를 이용해 1부터 100까지 총 100개의 정수로 채워진 배열을 만들고, random 모듈의 choice(..

01-16 최소 제곱법과 추세선 선형 회귀 def) 선형 회귀 (Linear Regression): 주어진 데이터를 가장 잘 설명하는 합리적인 선형함수를 찾는 문제 어떤 한 상인의 노동 시간에 따른 매출액 데이터가 있다고 해보겠습니다. 하루 노동 시간 매출 1 25000 2 55000 3 75000 4 110000 5 128000 6 155000 8 210000 이 표에서 7시간을 일했을 때의 매출액과 9시간 이상 일을 했을 때의 매출액은 나타나있지 않습니다. 그렇다면 주어진 데이터를 바탕으로 7시간, 9시간 일했을 때의 매출액을 예측하려면 어떻게 해야 할까요? 가장 간단한 방법은 주어진 데이터들 간의 상관관계를 선형함수의 형태로 나타내는 겁니다. 이를 선형 회귀라고 합니다. 대개 선형 회귀는 학습 데이..

01-15 편향과 오차 편향 이 세상에서 제일 무서운 사람은 많이 읽는 사람 아니야. 안 읽는 사람 아니야. 한 권 읽는 사람의 철학이 제일 무서운 거야! 강호동, 유튜브 웹 예능 라끼남 중 (출처: https://www.youtube.com/watch?v=LJ1vo48x5iY&list=PLr0T5CaHaPwVPDht_lnVaFvQCz4q5CpJc&index=29) def) 편향 (bias): 한쪽으로 치우침 사람이 어느 한 가지 분야에만 오로지 관심을 가질 때 생길 수 있는 부작용 중 하나로, 시야가 너무 편협해진다는 점이 있습니다. 위의 강호동의 말처럼 평생 책을 단 한 권만 읽은 사람은 오로지 그 책의 말에 따라 사고하고 판단할 것입니다. ML에서도 이 진리 격언은 그대로 쓰여서, 편향된 데이터(b..

01-14 최대 가능도 추정 모든 확률분포에 대한 모수를 완벽하게 추정할 수 있는 것은 아닙니다. ML에서도 이는 마찬가지여서 주어진 데이터가 우리가 알고 있는 확률분포를 완벽하게 따른다는 보장이 없습니다. 성능이 좋은 ML 알고리즘은 이러한 확률분포를 계산할 때 가장 그 경향성을 잘 모사하는 모수를 찾게 마련입니다. 이를 모수 추정 문제라고 합니다. 이 때, 모멘트 방법 이외에 이론상 가장 가능성이 높은 모수를 찾는 방법으로 최대 가능도 추정을 사용합니다. 어떤 확률변수 $X$에 대한 확률함수 $p\left(x;\theta\right)$에서 가지고 있는 데이터 $x$를 토대로 모수 $\theta$를 찾는 문제로 이해할 수 있습니다. 즉, 확률밀도함수에서 모수를 변수로 간주하는 겁니다. 이러한 문제 정의..

01-13 확률분포의 추정 지금까지는 확률분포가 주어져 있을 때 이를 이용한 확률의 계산과 그와 관련된 통계적인 지식을 배웠습니다. 하지만 현실에서는 확률분포함수로부터 나온 데이터만을 알 수 있는 경우가 많습니다. 따라서 데이터로부터 확률분포함수를 역으로 알아내는 과정이 필요하며, 이 일련의 과정을 추정(estimation)이라고 합니다. 추정과 기본적인 방법 def) 추정 (estimation): 가지고 있는 데이터로부터 확률분포를 추정하는 기술 궁극적으로 우리는 현재 주어진 데이터 이외의 데이터까지도 포괄적으로 설명해주는 확률분포를 아는 것이 목적입니다. 따라서 현재 주어진 데이터는 확률변수의 분포를 계산하여 추정하기 위한 도구로 보시면 되겠습니다. 사실 덮어놓고 데이터를 이용해 확률분포를 계산할 수..

01-12 공분산과 상관계수 분산이 어떤 데이터로부터 평균까지의 편차를 기반으로 한 데이터였다는 것을 지난 포스트에서 알아봤습니다. 이번에는 확률변수가 여러 개일 때로 상황을 바꿔서 데이터의 분포를 나타내보도록 하겠습니다. 공분산 def) 공분산 (Covariance): 다변수 데이터가 평균으로부터 얼마나 멀리 떨어져 있는지를 나타내는 척도 공분산 공식은 아래와 같이, 분산을 2차원으로 확장시킨 것과 같은 모습을 띕니다. $$s_{xy}=\frac{1}{N}\sum_{i=1}^N\left(x_i-\mu_x\right)\left(y_i-\mu_y\right)$$ 다만, 하나의 확률변수에 대해서는 평균값의 위치와 표본 위치의 거리로 나타낸 것과 다르게, 공분산은 평균값과 표본을 연결하는 사각형의 면적과 같습..

01-11 분산과 표준편차 통계에서 평균이나 중앙값은 어떤 데이터를 대표하는 값이라 할 수 있습니다. 그런데 과연 평균 또는 중앙값만으로 그 데이터의 모든 것을 설명할 수 있을까요? 실제 데이터의 평균과 중앙값 못지 않게 중요한 요소는 데이터가 평균 또는 중앙값을 기준으로 얼마나 조밀하게 뭉쳐서 또는 넓게 퍼져서 분포해 있는지를 나타내는 것입니다. 분산 def) 분산 (Variance): 평균과 관측치에 대한 편차(difference) 제곱의 평균값 평균을 기준으로 데이터가 얼마나 넓게 퍼져있는지를 나타내는 지표인 분산은 평균 $\mu$가 주어졌을 때 아래와 같이 계산할 수 있습니다. $$Var=\frac{1}{N}\sum_{i=1}^{N}\left|x_i-\mu\right|^2$$ 공식을 보면 평균으로..