01-10 평균과 기대값
통계라고 하면 가장 먼저 떠오르는 지표는 평균이 아닐까 합니다. 그만큼 가장 직관적이고 간단한 방법이라는 뜻이겠죠. 이번 포스트에서는 평균 그리고 이와 함께 쓰이는 대표적인 몇몇 지표들을 함께 정리해보겠습니다.
평균
평균(Mean)에는 산술 평균, 기하 평균, 조화 평균 등 여러 종류가 있지만 여기서는 가장 널리 쓰이는 산술 평균을 위주로 설명해보겠습니다.
def) 산술 평균(Arithmetic Mean): 모든 변수의 합을 그 개수만큼 나눠서 얻을 수 있는 대표값
$$A.M.=\frac{1}{n}\sum_{i}^{n}a_i=\frac{a_1+a_2+\cdots + a_n}{n}$$
가장 널리 쓰이고 가장 먼저 배우는 평균입니다. 위의 정의는 이산확률변수에 대해서 정리한 것이기 때문에 $\sum$ 기호를 사용한 것이고, 연속확률변수일 때는 적분 기호로 바꿔주면 됩니다.
$$A.M.=\frac{1}{n}\int_{a_1}^{a_n}X dx$$
특정한 집단을 대표하는 값
그럼 이쯤에서 한 번 짚고 넘어갈 문제를 보겠습니다. 과연 평균은 한 집단에 대한 데이터를 대표하기에 적절한 데이터일까요? 뉴스 등에서 어느 나라의 평균 소득은 증가했지만 서민 경제는 나아지지 않았다는 소식을 심심찮게 보셨을 겁니다. 이렇게 되는 이유는 상위 1%에 해당하는 특정 계층의 소득이 비대칭적으로 높기 때문에 서민층의 소득이 거의 변화하지 않았음에도 나라 전체의 소득이 증가한 것처럼 보이는 것이죠. 이와 같이 산술 평균은 극단적인 값, 통칭 아웃라이어(outlier)에 영향을 많이 받습니다. 이런 점에서 미루어볼 때 (산술)평균만으로 한 집단의 데이터를 표현하기에는 조금 성급한 감이 있습니다. 그래서 아웃라이어에 영향을 덜 받는 몇 가지 개념 중 중앙값과 기대값이 사용됩니다.
파이썬에서 평균을 구하는 몇 가지 방법들
넘어가기에 앞서 파이썬에서는 평균을 어떻게 구하는지를 알아보고 가겠습니다. 산술 평균의 정의대로 계산하는 방법과 라이브러리에서 제공하는 함수를 이용하는 방법이 있습니다.
import numpy as np
arr = np.array(range(5))
print(arr)
print(sum(arr)/len(arr))라이브러리를 이용할 때는

보통 넘파이를 사용하기 마련이지만 파이썬에 내장된 라이브러리인 math나 statistics를 이용하는 방법도 있다고 합니다.
import numpy as np
arr = np.array(range(5))
print(np.mean(arr))import statistics
print(statistics.mean(arr))
중앙값, 그리고 평균과의 비교
def) 중앙값(Median): 주어진 값들을 순서대로 정렬했을 때, 가장 중앙에 위치하는 값
크기 순대로 정렬한 후에 제일 가운데 값을 뽑는 것을 의미합니다. 평균과 비교하면 이 친구는 어떤 면에서 좋을까요? 앞서 예로 들었던 아웃라이어를 포함하는 데이터의 예를 들어보겠습니다. 아래 그림의 데이터를 보시면 되겠습니다.
import numpy as np
import matplotlib.pyplot as plt
a = [1, 1.5, 1.8, 2.0, 3.0, 7.23, 11.7, 12.0, 10.0, 1.0]
avg_a = np.mean(a)
a_sorted = [1, 1.5, 1.8, 2.0, 3.0, 7.23, 11.7, 12.0, 10.0, 1.0]
a_sorted.sort()
med_a = a_sorted[len(a)//2 + 1]
plt.plot(range(len(a)), a, 'k-', marker='o', label='Raw data')
plt.plot(np.ones(len(a))*avg_a, np.linspace(0, 12, len(a)), 'b--', label='Arithmetic mean')
plt.plot(np.ones(len(a))*med_a, np.linspace(0, 12, len(a)), 'r--', label='Median')
plt.grid()
plt.legend(loc='upper left')
plt.title('Arithmetic mean and median of the given data', fontsize=13)
plt.show()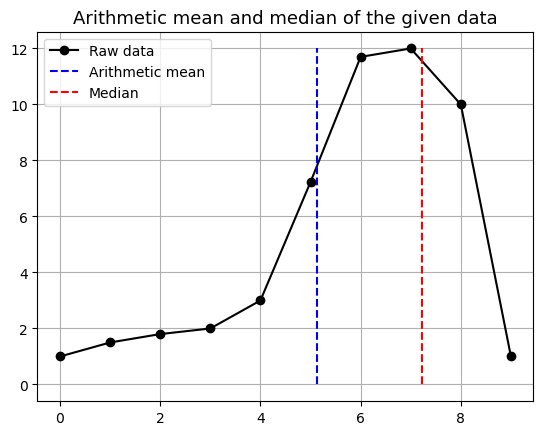
이 그래프에서 데이터는 오른쪽으로 치우친 것을 볼 수 있습니다. 이럴 경우, 평균은 그 데이터가 어떤 특성을 나타내는지를 잘 알려줄 수 없습니다. 반대로 중앙값은 한쪽으로 치우친 데이터를 비교적 잘 따라갑니다. 따라서 평균은 데이터의 분포가 정규분포와 같이 대칭적으로 분포할 때는 사용해도 괜찮지만, 그렇지 않고 비대칭 분포를 보이거나 아웃라이어가 존재한다면 중앙값 등의 다른 수치를 이용하는 것이 좋습니다.
기대값
def) 기대값(Expectation): 어떤 확률 과정을 무한히 반복했을 때, 얻을 수 있는 값의 평균으로서 기대할 수 있는 값. 각 사건에 대해 확률변수와 확률 값을 곱하여 그것들의 합을 취한 값.
사실 기대값은 그 값만 놓고 보았을 때 평균과 같을 수도 있습니다. 엄밀하게 정의하면, 특정 확률변수에 해당하는 확률값을 일종의 가중치(weight)로 간주하는 가중 평균이라고도 할 정도니까요. 이산확률변수와 연속확률변수에 대하여 각각 기대값을 구하는 방법은 아래와 같습니다.
$$E\left[X\right]=\sum_{i}x_i\cdot f\left(x_i\right)$$
$$E\left[X\right]=\int_{-\infty}^{\infty}x\cdot f\left(x\right)dx$$
평균과 기대값의 비교
앞서 기대값과 평균을 혼용해서 사용하는 단어라고 하기는 했지만, 일반적으로 이 두 단어는 사용되는 문맥이 다릅니다.
평균은 이미 주어진 값 에 대하여 통계적인 특성을 분석할 때 사용됩니다. 반대로 기대값은 새로운 데이터가 관측되었을 때 그 데이터가 확률적으로 어떤 값을 가질지를 예측하는 데 사용됩니다.
10일차 후기
어느덧 며칠째 공부했는지 나타내는 숫자가 두 자릿수가 되었네요. 기왕 습관 잡는 거 열심히 해서 제대로 배워가야 겠습니다. 그리고 지금은 환급 챌린지 때문에 수학적 내용에다가 파이썬을 덧붙이는 내용으로 적었는데, 나중에 내용을 분리시켜서 수학적 이론은 이론대로, 코드는 코드대로 별도의 포스트를 만들려고 합니다.
패스트캠퍼스 [직장인 실무교육]
프로그래밍, 영상편집, UX/UI, 마케팅, 데이터 분석, 엑셀강의, The RED, 국비지원, 기업교육, 서비스 제공.
fastcampus.co.kr
* 본 포스팅은 패스트캠퍼스 환급 챌린지 참여를 위해 작성되었습니다.
'[패스트캠퍼스 환급챌린지]딥러닝 > Chapter 1. 통계' 카테고리의 다른 글
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-12 공분산과 상관계수 (0) | 2023.03.03 |
|---|---|
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-11 분산과 표준편차 (0) | 2023.03.02 |
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-09 베이즈 정리 (0) | 2023.02.28 |
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-08 조건부확률 (0) | 2023.02.27 |
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-07 결합확률과 주변확률 (1) | 2023.02.26 |