01-11 분산과 표준편차
통계에서 평균이나 중앙값은 어떤 데이터를 대표하는 값이라 할 수 있습니다. 그런데 과연 평균 또는 중앙값만으로 그 데이터의 모든 것을 설명할 수 있을까요? 실제 데이터의 평균과 중앙값 못지 않게 중요한 요소는 데이터가 평균 또는 중앙값을 기준으로 얼마나 조밀하게 뭉쳐서 또는 넓게 퍼져서 분포해 있는지를 나타내는 것입니다.
분산
def) 분산 (Variance): 평균과 관측치에 대한 편차(difference) 제곱의 평균값
평균을 기준으로 데이터가 얼마나 넓게 퍼져있는지를 나타내는 지표인 분산은 평균 $\mu$가 주어졌을 때 아래와 같이 계산할 수 있습니다.
$$Var=\frac{1}{N}\sum_{i=1}^{N}\left|x_i-\mu\right|^2$$
공식을 보면 평균으로부터의 편차를 단순히 더하지 않고 제곱을 합니다. 왜냐하면 평균과의 차이를 단순히 더해버리면 그 값은 0이 되기 때문입니다. 분산이 작으면 각 데이터가 평균에 가까이 위치해 가늘고 날카로운 분포 곡선을 보입니다. 반대로 분산이 클수록 더 넓게 퍼진 개형의 곡선을 가집니다. 또한, 데이터의 분포 양상은 아래 두 그림에서 볼 수 있듯이 평균에 영향을 받지 않고, 오로지 분산(정확히는 아래에서 설명할 표준편차)에 의해서만 달라집니다.
import numpy as np
import matplotlib.pyplot as plt
mu = 0.0
sigma = [1.0, 3.0]
x = np.linspace(-5, 5, 100)
plt.figure(figsize=(8,4))
for s in sigma:
plt.plot(x, (1 / np.sqrt(2 * np.pi * s**2)) * np.exp(-(x-mu)**2 / (2 * s**2)), linewidth=3, label='$\sigma$='+f'{s}')
plt.xlabel('x', fontsize=12)
plt.ylabel('f(x)', fontsize=12)
plt.legend(loc='upper left')
plt.grid()
plt.show()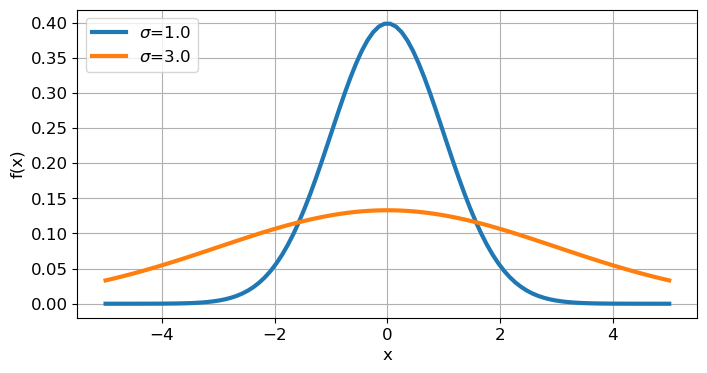
mu = 1.5
sigma = [1.0, 3.0]
x = np.linspace(-5, 5, 100)
plt.figure(figsize=(8,4))
for s in sigma:
plt.plot(x, (1 / np.sqrt(2 * np.pi * s**2)) * np.exp(-(x-mu)**2 / (2 * s**2)), linewidth=3, label='$\sigma$='+f'{s}')
plt.xlabel('x', fontsize=12)
plt.ylabel('f(x)', fontsize=12)
plt.legend(loc='upper left')
plt.grid()
plt.xlim([-6, 6])
plt.show()
표준편차
def) 표준편차(Standard Deviation): 분산의 양의 제곱근
사실 데이터의 분포를 나타나는 데 마냥 분산만 사용하기에는 제약이 있습니다. 편차의 제곱을 사용하기 때문에 데이터가 멀리 떨어져있다면 값이 끝을 모르고 커질 수 있기 때문이죠. 따라서 제곱한 값을 다시 원래의 크기로 표준화 할 필요가 있습니다. 이를 표준편차라고 하며, 정의는 아래와 같습니다.
$$\sigma=\sqrt{Var}=\sqrt{\frac{1}{N}\sum_{i=1}^{N}\left|x_i-\mu\right|^2}$$
파이썬에서의 적용
평균을 구현하는 방법이 다양하게 구현되어 있듯이, 분산과 표준편차도 파이썬에서 다양한 방법으로 계산할 수 있습니다. 먼저 정의대로 계산해서 직접 얻는 방법입니다. 단, 제곱근을 계산하기 위해 math 라이브러리의 sqrt 메서드만 따로 호출했습니다.
import math
arr = [56, 93, 88, 72, 65]
mean = 0
for x in arr:
mean += x / len(arr)
variance = 0
for x in arr:
variance += ((x-mean)**2) / len(arr)
std = math.sqrt(variance)
print(f"Mean: {mean:.2f}")
print(f"Variance: {variance:.2f}")
print(f"Standard deviation: {std:.2f}")Mean: 74.80
Variance: 192.56
Standard deviation: 13.88두번째는 넘파이로 구현하는 방법입니다. 넘파이에는 분산과 표준편차를 계산하는 메서드가 각각 따로 구현되어 있습니다.
import numpy as np
print(f"Variance: {np.var(arr):.2f}")
print(f"Standard deviation: {np.std(arr):.2f}")Variance: 192.56
Standard deviation: 13.8811일차 후기
5시 즈음에 패스트캠퍼스에서 문자가 왔습니다. 1주차 미션 성공...!!
다행히도 오타나 그런 거 없었나 보다
이 기세로 한 달 전부 채워보겠습니다.
열심히 살겠습니다
패스트캠퍼스 [직장인 실무교육]
프로그래밍, 영상편집, UX/UI, 마케팅, 데이터 분석, 엑셀강의, The RED, 국비지원, 기업교육, 서비스 제공.
fastcampus.co.kr
* 본 포스팅은 패스트캠퍼스 환급 챌린지 참여를 위해 작성되었습니다.
'[패스트캠퍼스 환급챌린지]딥러닝 > Chapter 1. 통계' 카테고리의 다른 글
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-13 확률분포의 추정 (0) | 2023.03.04 |
|---|---|
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-12 공분산과 상관계수 (0) | 2023.03.03 |
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-10 평균과 기대값 (0) | 2023.03.01 |
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-09 베이즈 정리 (0) | 2023.02.28 |
| [패스트캠퍼스][환급 챌린지]Chapter 1. 딥러닝을 위한 통계 01-08 조건부확률 (0) | 2023.02.27 |