02-09 우선순위 큐
우선순위 큐는 다양한 알고리즘 및 프로그램에서 사용 빈도가 높은 중요한 구조입니다. 이번 포스트에서는 우선순위 큐에 대한 일반적인 얘기를 먼저 한 뒤, 우선순위 큐의 가장 대표적인 예시인 힙(heap)을 알아보겠습니다.
우선순위 큐
def) 우선순위 큐 (Priority Queue): 우선순위에 따라서 데이터를 추출하는 자료구조
우선순위 큐는 큐(queue) 자료구조의 변형 형태로 볼 수 있으며, 컴퓨터 운영체제(OS)나 온라인 게임 매칭 등에 사용되는 구조입니다. 운영체제의 경우, 우리가 음악을 들으면서 문서 작업을 하는 등 한 컴퓨터에서 여러 작업을 동시에 작동시키는 경우가 많습니다.
당장 저만 해도 블로그 정리할 때 항상 유튜브 브금을 깔아놓습니다
이 때 프로그램의 우선순위를 지정해서 실행시키는 데 이용하는 거죠.
이전까지 중요하게 다뤘던 스택(stack), 큐와 비교하면 아래 표와 같이 나타낼 수 있겠습니다.
| 자료구조 | 추출되는 데이터 |
|---|---|
| 스택 | 가장 나중에 삽입된 데이터 |
| 큐 | 가장 먼저 삽입된 데이터 |
| 우선순위 큐 | 가장 우선순위가 높은 데이터 |
우선순위 큐를 구현하는 방법
데이터의 개수가 $N$개일 때, 구현 방식에 따른 시간복잡도는 아래와 같습니다. 아래 표에서 힙은 좀 더 아래에서 설명하도록 하죠.
| 우선순위 큐 구현 방식 | 삽입 시간 | 삭제 시간 |
|---|---|---|
| 리스트 자료형 | $O\left(1\right)$ | $O\left(N\right)$ |
| 힙 (Heap) | $O\left(\log N\right)$ | $O\left(\log N\right)$ |
예전에 큐를 다룬 포스트에서 일반적인 큐는 선형적인 구조를 가졌음을 알 수 있었습니다. 반면, 우선순위 큐는 지난 포스트에서 언급한 바 있는 이진 트리 구조를 사용합니다. 이 때문에 비선형적인 자료구조에 해당하며, 따라서 리스트 자료구조와는 본질적인 차이가 있습니다.
포화 이진 트리
힙에 대해 알기 전에 몇 가지 이진 트리 구조를 좀 더 알아보겠습니다.
def) 포화 이진 트리 (Full Binary Tree): 리프 노드를 제외한 모든 노드가 두 개의 자식 노드를 가지고 있는 트리
완전 이진 트리
def) 완전 이진 트리 (Complete Binary Tree): 모든 노드가 왼쪽 자식부터 차근차근 채워진 트리
아래에서 개념이 다시 나오는 트리이니 잘 알아두세요! 아래 그림은 완전 이진 트리의 정의에 맞게 이를 구성하는 과정을 나타낸 것입니다.
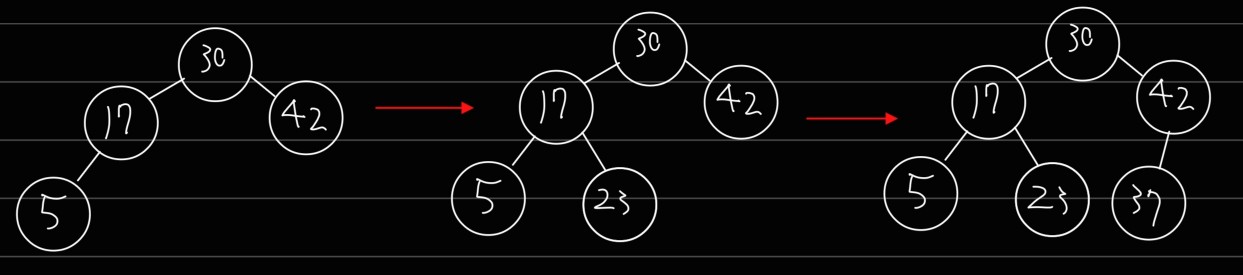
높이 균형 트리
def) 높이 균형 트리 (Height Balanced Tree): 양쪽 서브 트리의 높이가 1 이상 차이 나지 않는 트리

힙
def) 힙 (Heap): 원소들 중에서 최대값 또는 최소값을 빠르게 찾아내는 자료구조
이제 본격적으로 힙에 대해서 알아보겠습니다. 힙은 최대 원소를 추출하거나 최소 원소를 추출하는 자료구조입니다. 위의 표에서 잠시 짚고 넘어갔다시피 힙은 원소의 삽입과 삭제에 $O\left(\log N\right)$의 수행 시간을 요구합니다. 또한, 단순한 $N$개의 데이터를 힙에 넣었다가 모두 꺼내는 작업은 정렬과 동일합니다. 이 때의 시간 복잡도는 $O\left(N\log N\right)$입니다.
최대 힙
def) 최대 힙 (Max Heap): 부모 노드가 자식 노드보다 값이 큰 완전 이진 트리
이 때문에 최대 힙의 루트 노드는 전체 트리에서 가장 큰 키 값을 가진다는 특징이 있습니다.
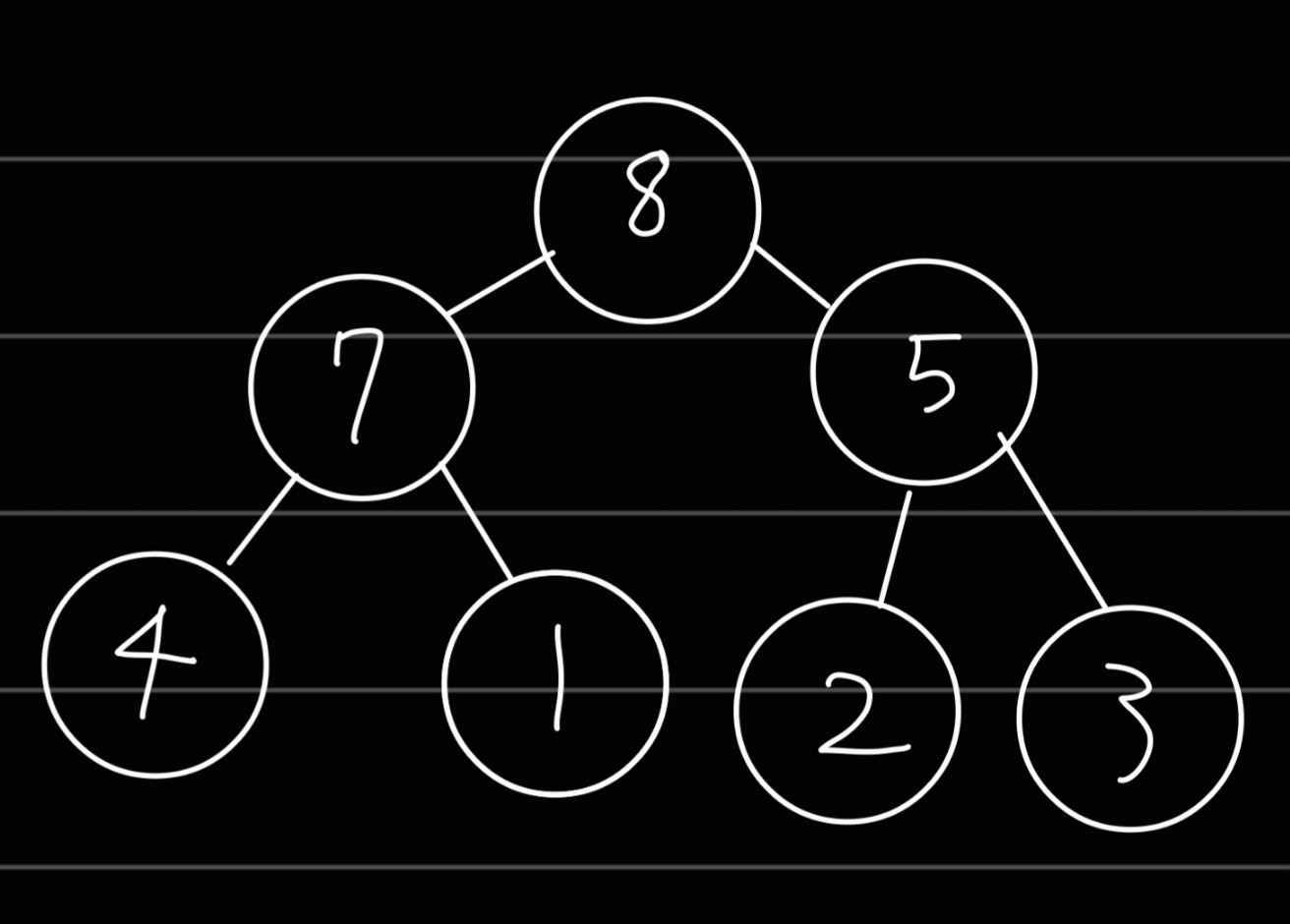
힙의 특징
여기까지 알아본 힙의 특징을 정리해보겠습니다. 힙은 완전 이진 트리 자료구조를 따르며, 우선순위가 높은 노드가 루트에 위치한다는 특징이 있습니다. 우리가 뽑아내고자 하는 값이 최대인지 최소인지에 따라서 최대 힙과 최소 힙을 구분됩니다. 이들 각각의 특징을 정리하면...
- 최대 힙: 부모 노드의 키(key) 값이 자식 노드의 키 값보다 항상 크고, 루트 노드가 가장 크며, 값이 큰 데이터가 우선순위가 높음.
- 최소 힙: 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작고, 루트 노드가 가장 작으며, 값이 작은 데이터가 우선순위가 높음.
과 같은 특징이 있습니다.
최소 힙 구성 함수: Heapify
이 중에서 최소 힙을 구성하는 함수는 heapify라는 이름으로 구현됩니다. 이 함수는 노드의 키 값에 대하여 상향식으로, 즉 자식으로부터 부모로 거슬러 올라가며, 부모보다 자식의 키 값이 더 작은 경우에 위치를 서로 교체해줍니다.
힙에 새로운 원소가 삽입될 때
실제로 힙의 연산이 어떻게 되는지 예제로 알아보겠습니다. 최소 힙을 기준으로 설명해보죠. 균형 잡힌 이진 트리이기 때문에 새로운 원소가 삽입되었을 때 $O\left(\log N\right)$ 시간복잡도를 가져 힙의 성질을 유지시킬 수 있습니다.
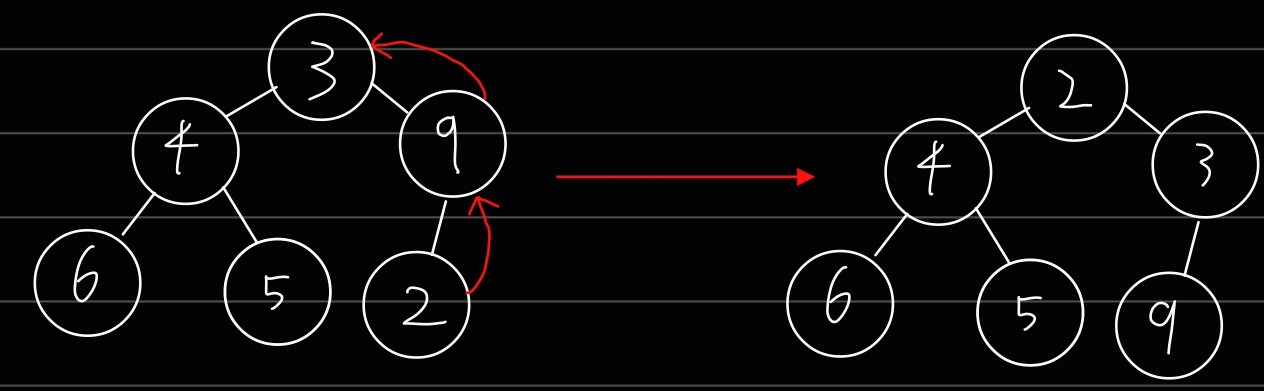
힙에서 원소를 삭제할 때
원소를 제거할 때는 가장 마지막 노드가 루트 노드의 위치에 오도록 바꿔줍니다. 이후 루트에서부터 하향식으로, 즉 더 작은 자식 노드로 Heapify()를 진행합니다.
그럼 다시 한 번 힙의 특징을 정리하고 넘어가겠습니다. 힙의 삽입과 연산을 수행할 때, 노드를 거슬러 올라갈 때 혹은 내려갈 때마다 처리할 범위에 포함된 원소의 개수가 절반씩 줄어듦을 직관적으로 알 수 있습니다. 따라서 삽입과 삭제에 대한 시간 복잡도가 $O\left(\log N\right)$가 되는 것입니다.

파이썬의 힙(Heap) 라이브러리
파이썬에서는 어떻게 구현되는지 알아보죠. 파이썬에서는 heapq 라이브러리를 이용합니다. 시간복잡도는 위에서 설명한 것과 같이 삽입 및 삭제에 대하여 $O\left(\log N\right)$입니다.
특이하게도 단순히 하나의 빈 리스트를 만들면, 그것을 그대로 힙 자료구조로 사용할 수가 있습니다.
import heapq
heap = []
print(heap)힙에 원소를 삽입하고 힙으로부터 원소를 추출할 때는 각각 heappush(), heappop() 메서드를 사용합니다.
import heapq
heap = []
heapq.heappush(heap, 7)
heapq.heappush(heap, 4)
heapq.heappush(heap, 5)
heapq.heappush(heap, 8)
while heap:
element = heapq.heappop(heap)
print(element, end=" ")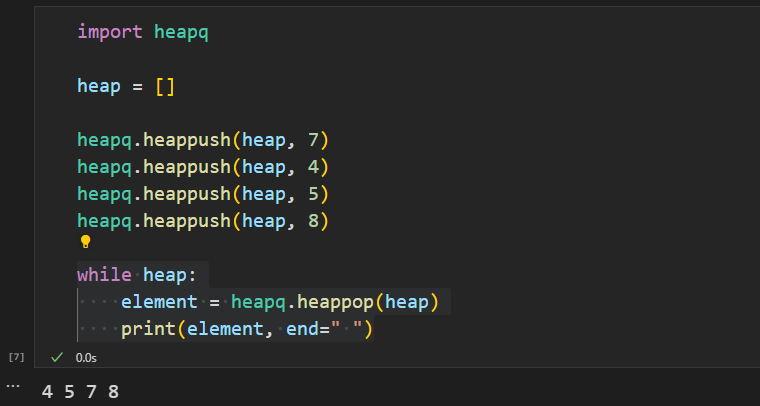
출력 결과를 보면 원소들이 오름차순으로 정렬되어 있는 것을 확인할 수 있습니다. 따라서 최소값과 최대값을 구할 때는 단순히 슬라이싱 기능으로 맨 앞, 맨 뒤 원소를 출력하면 그만입니다.
import heapq
heap = []
heapq.heappush(heap, 7)
heapq.heappush(heap, 4)
heapq.heappush(heap, 5)
heapq.heappush(heap, 8)
print(heap[0])
print(heap[-1])
한편, 굳이 heappush() 메서드를 이용하지 않고 이미 만들어져있는 리스트 등을 힙으로 변환하는 방법도 있습니다. heapify() 메서드를 사용하면, 새로운 리스트를 반환하지 않고, 리스트 내부를 직접 수정합니다.
import heapq
heap = [9, 1, 5, 4, 3, 8, 7]
heapq.heapify(heap)
while heap:
element = heapq.heappop(heap)
print(element, end=" ")
위에서 본 것처럼 heapq 라이브러리는 기본적으로 최소 힙 기능을 제공합니다. 만약 최대 힙을 사용하고 싶다면 (삽입과 추출할 때 모두) 키에 음수 부호(-)를 붙여야 합니다.
import heapq
arr = [9, 1, 5, 4, 3, 8, 7]
heap = []
for x in arr:
heapq.heappush(heap, -x)
while heap:
x = -heapq.heappop(heap)
print(x, end=" ")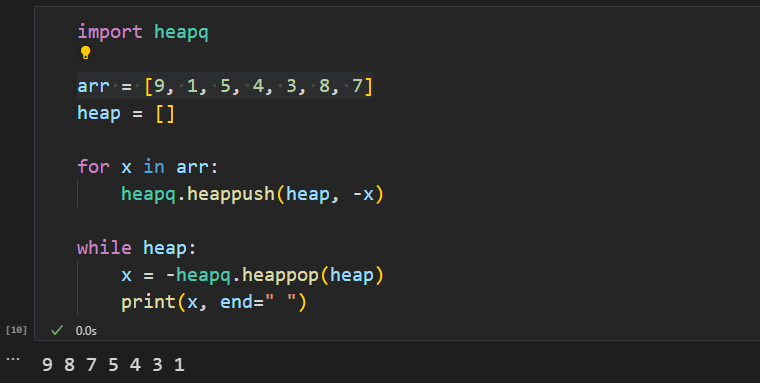
활용 예시
Case 1. 힙 정렬 (Hip Sort)
위에서도 한 번 다뤘던 예시인데요, 단순히 힙에 원소를 넣었다가 꺼내는 것만으로도 정렬을 수행할 수 있습니다. 차이점이 있다면, 위의 예시에서는 아무 것도 반환하지 않지만, 이번에는 정렬이 끝난 리스트를 result라는 이름의 변수로 저장해서 반환하게 만들어져 있습니다.
import heapq
def heap_sort(arr):
heap = []
for x in arr:
heapq.heappush(heap, x)
result = []
while heap:
x = heapq.heappop(heap)
result.append(x)
return result
arr = [9, 1, 5, 4, 3, 8, 7]
print(heap_sort(arr))
Case 2. N번째로 작은 값
최소/최대 힙 기능의 연장선으로 $n$번째로 작은 값/큰 값을 출력할 수도 있습니다. 기본적인 아이디어는 힙 자료구조를 만든 뒤에 heappop() 함수를 $n$번 호출하는 겁니다.
import heapq
def n_smallest(n, arr):
heap = []
for x in arr:
heapq.heappush(heap, x)
result = None
for _ in range(n):
result = heapq.heappop(heap)
return result
arr = [9, 1, 5, 4, 3, 8, 7]
print(n_smallest(3, arr))
이렇게 직접 정의하는 방법 외에도 이미 라이브러리에 nsmallest() 메서드가 만들어져 있습니다. 이 메서드는 가장 작은 $n$개의 값을 반환하므로 맨 마지막 원소를 출력하면 그 원소가 $n$번째로 작은 원소입니다.
import heapq
arr = [9, 1, 5, 4, 3, 8, 7]
result = heapq.nsmallest(3, arr)
print(result[-1])
Case 3. N번째로 큰 값
마찬가지로 $n$번째로 큰 값을 구할 때는 nlargest() 메서드를 사용합니다.
import heapq
arr = [9, 1, 5, 4, 3, 8, 7]
result = heapq.nlargest(3, arr)
print(result[-1])
파이썬에서의 구현
class Heap(object):
def __init__(self):
# Do not use the first element
self.arr = [None]
def push(self, x):
self.arr.append(x)
if len(self.arr) == 2:
return
i = len(self.arr) - 1
while True:
parent = i // 2
if 1 <= parent and self.arr[parent] > self.arr[i]:
self.arr[parent], self.arr[i] = self.arr[i], self.arr[parent]
i = parent
else:
break
def pop(self):
i = len(self.arr) - 1
if i < 1:
return None
self.arr[1], self.arr[i] = self.arr[i], self.arr[1]
result = self.arr.pop()
self.heapify()
return result
def heapify(self):
if len(self.arr) <= 2:
return
i = 1
while True:
child = 2 * i
if child + 1 < len(self.arr):
if self.arr[child] > self.arr[child+1]:
child += 1
if child >= len(self.arr) or self.arr[child] > self.arr[i]:
break
# Replace elements, and descends towards child
self.arr[i], self.arr[child] = self.arr[child], self.arr[i]
i = child
arr = [9, 1, 5, 4, 3, 8, 7]
heap = Heap()
for x in arr:
heap.push(x)
while True:
x = heap.pop()
if x == None:
break
print(x, end=" ")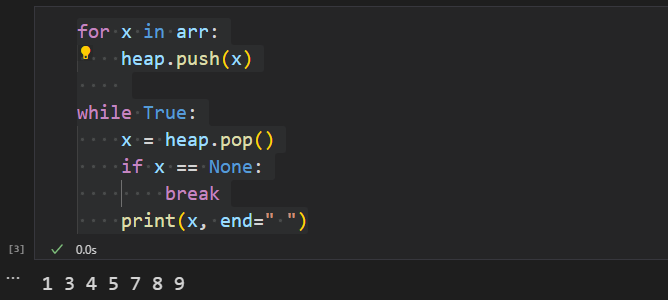
실행 시간을 비교해보겠습니다.
import random, time
arr = []
n = 10 ** 5
for _ in range(n):
arr.append(random.randint(0, 10 ** 6))
start_time = time.time()
heap = Heap()
for x in arr:
heap.push(x)
result = []
while True:
x = heap.pop()
if x == None:
break
result.append(x)
print(f"Elapsed time: {time.time() - start_time} seconds.")
ascending = True
for i in range(n-1):
if result[i] > result[i+1]:
ascending = False
print("Sorted:", ascending)
print(result[:5])
print(result[-5:])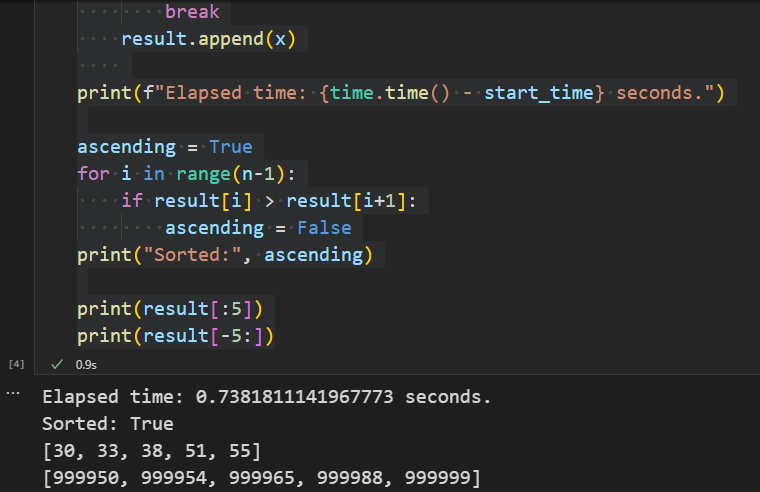
26일차 후기
바로 어제, 3주차 미션의 성공 여부를 문자로 확인받기로 했던 날이었습니다. 분명 일요일 날 설문지에 블로그 글 기록을 적을 때까지만 해도 3월 16일 오후 7시까지는 보내주기로 했는데 8시가 다 되도록 감감무소식이었죠.
결국 아침에 일어나면 물어봐야 겠다 했는데, 오전 10시 즈음에 검수가 늦어져 오늘 14시까지 알려주겠다는 문자와 메일이 왔습니다. 그리고 10분도 안 되어서 성공 판정 문자가 왔습니다. 실패한 줄...
놀래라
패스트캠퍼스 [직장인 실무교육]
프로그래밍, 영상편집, UX/UI, 마케팅, 데이터 분석, 엑셀강의, The RED, 국비지원, 기업교육, 서비스 제공.
fastcampus.co.kr
* 본 포스팅은 패스트캠퍼스 환급 챌린지 참여를 위해 작성되었습니다.
'[패스트캠퍼스 환급챌린지]딥러닝 > Chapter 2. 자료구조' 카테고리의 다른 글
| [패스트캠퍼스][환급 챌린지]Chapter 2. 딥러닝을 위한 자료구조 02-10 그래프의 표현 (0) | 2023.03.18 |
|---|---|
| [패스트캠퍼스][환급 챌린지]Chapter 2. 딥러닝을 위한 자료 구조 02-08 이진 탐색 트리 (0) | 2023.03.16 |
| [패스트캠퍼스][환급 챌린지]Chapter 2. 딥러닝을 위한 자료구조 02-07 덱 (1) | 2023.03.15 |
| [패스트캠퍼스][환급 챌린지]Chapter 2. 딥러닝을 위한 자료구조 02-06 큐 (0) | 2023.03.14 |
| [패스트캠퍼스][환급 챌린지]Chapter 2. 딥러닝을 위한 자료구조 02-05 스택 (0) | 2023.03.13 |