02-10 그래프의 표현
드디어 자료구조의 마지막 파트입니다. 자료구조 이야기하다가 뜬금없이 그래프 얘기가 나와서 처음엔 '....?' 싶었습니다. 그게 우리가 아는 그래프랑 조금 다른 개념까지 포괄하는 것을 깨닫는 데는 단 5분도 걸리지 않았습니다... 애초에 그래프 자료구조를 얘기하기는 것이기도 했고 말이죠.
딥러닝 분야에는 GCN(Graph Convolutional Network)라는 학습 알고리즘이 따로 존재할 정도니 이번 파트도 잘 배워보죠.
그래프
def) 그래프 (Graph): 사물을 정점(vertex 또는 node)과 간선(edge)으로 나타내기 위한 도구
그래프를 수치적으로 나타나는 데에는 크게 2가지 방식이 있습니다.
- 인접 행렬(adjacency matrix): 2차원 배열을 사용하는 방식
- 인접 리스트(adjacency list): 연결 리스트를 사용하는 방식
풀어서 설명을 하자면, 첫 번째의 인접 행렬 방식은 두 노드가 연결되어 있는지 아닌지의 여부를 행렬(matrix)로 나타내는 겁니다.
인접 리스트에서는 각각의 노드마다 리스트를 만들어서, 그 노드가 어떤 노드와 연결되어 있는지 나타냅니다.
인접 행렬
인접 행렬에서는 그래프를 2차원 배열로 표현한다고 했습니다. 아래 그림을 예로 들어보죠.
0, 1, 2의 세 노드로 구성되어 있고, 간선은 0과 1을 잇는 3, 그리고 0과 2를 잇는 7의 총 2개입니다. 이를 2차원 배열로 나타내면 아래와 같습니다. 노드 1과 2를 잇는 간선이 없기 때문에 이 부분은 무한($\infty$)으로 표시합니다.
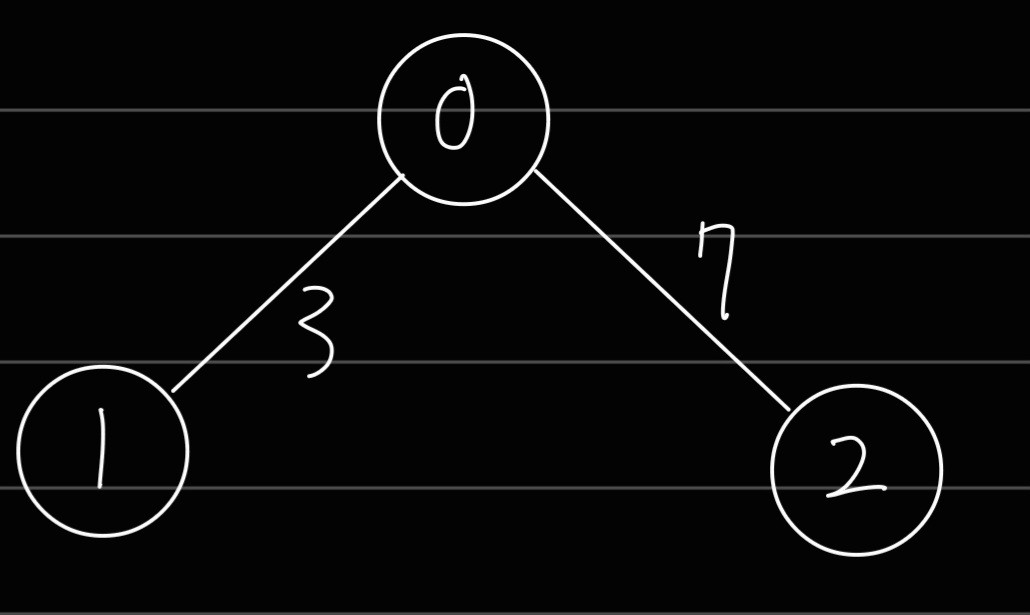
$$\begin{bmatrix} 0 & 3 & 7 \\ 3 & 0 & \infty \\ 7 & \infty & 0\end{bmatrix}$$
인접 행렬 - 무방향 무가중치 그래프
def) 무방향 그래프: 모든 간선이 방향성을 가지지 않는 그래프
무가중치 그래프: 모든 간선에 가중치가 없는 그래프
그래프 중에서는 몇 가지 특성을 가지는 것들이 있습니다. 무방향과 무가중치가 그것인데요. 무방향에서 모든 간선이 방향성을 가지지 않는다는 뜻은, 어떤 간선이 노드 0과 1을 잇는다고 하면 그 간선을 따라서는 0에서 1로 가든, 1에서 0으로 가든 상관없음을 의미합니다. 무가중치는 간선에 1 이외의 수치가 부여되지 않음을 뜻합니다. 위의 인접행렬 예제에서는 간선에 각각 3과 7이라는 가중치가 부여되어 있습니다.
이러한 특성을 지닌 그래프는 인접행렬 형태로 출력할 수 있다는 특징이 있습니다. 주의할 점은 어떤 그래프에서 정점의 개수가 $n$개라고 할 때, 인접 행렬은 반드시 $n\times n$의 차원을 가져야 합니다. 아래 그래프를 인접 행렬로 나타내면 다음 코드와 같습니다. 노드가 0, 1, 2, 3으로 총 네 개이기 때문에 $4\times 4$행렬로 표현되었습니다.

graph = [
[0, 1, 1, 0],
[1, 0, 1, 0],
[1, 1, 0, 1],
[0, 0, 1, 0]
]실제로 그래프에서 정점을 표현할 경우에는 정점에 V라는 표시를 해주기도 합니다. 영문 명칭인 vertex에서 따온 것이라고 하네요.
인접 행렬 - 방향 가중치 그래프
이번에는 정반대의 특성을 가지는 그래프입니다. 모든 간선이 방향을 가지고, 모든 간선에 가중치가 있는 그래프입니다. 아래 그림의 방향 가중치 그래프를 인접행렬로 나타내면 다음 코드와 같습니다. 간선 3을 예로 들어 설명해보죠. 보시는 것처럼 정점 1에서 0으로 갈 수는 있지만, 0에서 1로는 갈 수 없기 때문에 행렬의 1행 2열(0 to 1)은 0이고, 2행 1열(1 to 0)은 간선에 부여된 가중치 3이 됩니다.

graph = [
[0, 0, 7, 0],
[3, 0, 8, 0],
[0, 8, 0, 1],
[0, 0, 4, 0]
]인접 리스트
인접 행렬을 이용한 방식은 굳이 연결되지 않는 정점들까지 모두 공간을 할당해야 하기 때문에 상대적으로 메모리가 많이 소모되는 방식이 있습니다. 공간 효율성은 조금 떨어지는 셈이죠.
이에 반해 인접 리스트는 메모리를 훨씬 적게 소모하고, 특히 간선이 적은 그래프에 대해서 강점을 발휘할 수 있습니다. 아래 그래프는 인접 리스트로 표현하면 다음과 같습니다. 소괄호 안에서 첫번째 숫자는 연결된 정점을 뜻하며, 두번째 숫자는 해당 노드를 이어주는 간선의 가중치를 뜻합니다.

인접 리스트 - 무방향 무가중치 그래프
인접 행렬에서 예시로 들었던 그래프를 다시 불러옵시다. 이를 인접 리스트로 출력하면 아래 코드와 같습니다. 0번 정점은 1번과 2번 정점과 연결되어 있고, 1번 정점은 0번과 2번 정점, 2번 정점은 0, 1, 3의 세 노드와 모두 연결되어 있고, 3번 정점은 2번 정점하고만 연결되어 있음을 나타냅니다.

graph = [
[1, 2],
[0, 2],
[0, 1, 3],
[2]
]인접 리스트 - 방향 가중치 그래프
같은 방식으로 방향 가중치 그래프를 인접 리스트로 출력해보겠습니다. 첫번째 숫자로 정점을, 두번째 숫자로 간선의 가중치를 나타냅니다.

graph = [
[(2, 7)],
[(0, 3), (2, 8)],
[(1, 8)],
[(2, 4)]
]그래프의 공간/시간복잡도
지금까지 배운 것들을 종합해봅시다. 정점의 개수를 $V$, 간선의 개수를 $E$라고 하겠습니다. 기본적으로 인접 행렬은 모든 정점들의 연결 여부를 저장하기 때문에 $O\left(V^2\right)$의 공간을 요구합니다. 공간 효율성은 다소 떨어지죠? 하지만 두 노드의 연결 여부를 확인하는 데 $O\left(1\right)$의 시간 밖에 소요되지 않습니다.
한편, 인접 리스트는 연결된 간선의 정보만을 저장하므로 $O\left(V + E\right)$의 공간을 요구합니다(사실 일반적으로 $V\le E$이기 때문에 $O\left(V + E\right)$라고 해도 무리는 아닙니다). 인접 행렬과 비교했을 때 공간 효율성은 우수하지만, 두 노드의 연결 여부를 확인하려면 $O\left(V\right)$의 시간이 필요하므로 인접 행렬에 비해서는 비효율적입니다. 이를 표로 정리하면 아래와 같습니다.
| 필요한 메모리 | 연결 여부 확인 시간 | |
|---|---|---|
| 인접 행렬 | $O\left(V^2\right)$ | $O\left(1\right)$ |
| 인접 리스트 | $O\left(V + E\right)$ | $O\left(V\right)$ |
자료구조 챕터를 마치며
일반적으로 자료구조를 공부하면 자료구조의 종류와 특성, 그리고 그래프까지 다루게 됩니다. 그래프를 다루는 데 있어서 이를 어떻게 자료구조로 표현할 수 있는지까지 잘 숙지하심이 필요합니다. 여러모로 컴퓨터공학 비전공자에게 쉽지 않은 관문이지만 필요할 때마다 찾아보고 계속 복습해서 자기 것으로 체득해야 하겠습니다.
27일차 후기
자, 오늘로서 Chapter 2에 해당하는 자료구조까지 끝났습니다. 내일부터는 본격적으로 파이썬을 다루게 됩니다. 사실 Chapter 1, 2를 진행하면서 이미 파이썬을 이용해 코드를 짜 보기도 했지만, 이제는 파이썬 개발 환경의 세팅과 파이썬이라는 프로그래밍 언어 그 자체의 기본적인 사용방법을 알아보는 시간이 되겠습니다.
패스트캠퍼스 [직장인 실무교육]
프로그래밍, 영상편집, UX/UI, 마케팅, 데이터 분석, 엑셀강의, The RED, 국비지원, 기업교육, 서비스 제공.
fastcampus.co.kr
* 본 포스팅은 패스트캠퍼스 환급 챌린지 참여를 위해 작성되었습니다.
'[패스트캠퍼스 환급챌린지]딥러닝 > Chapter 2. 자료구조' 카테고리의 다른 글
| [패스트캠퍼스][환급 챌린지]Chapter 2. 딥러닝을 위한 자료구조 02-09 우선순위 큐 (0) | 2023.03.17 |
|---|---|
| [패스트캠퍼스][환급 챌린지]Chapter 2. 딥러닝을 위한 자료 구조 02-08 이진 탐색 트리 (0) | 2023.03.16 |
| [패스트캠퍼스][환급 챌린지]Chapter 2. 딥러닝을 위한 자료구조 02-07 덱 (1) | 2023.03.15 |
| [패스트캠퍼스][환급 챌린지]Chapter 2. 딥러닝을 위한 자료구조 02-06 큐 (0) | 2023.03.14 |
| [패스트캠퍼스][환급 챌린지]Chapter 2. 딥러닝을 위한 자료구조 02-05 스택 (0) | 2023.03.13 |